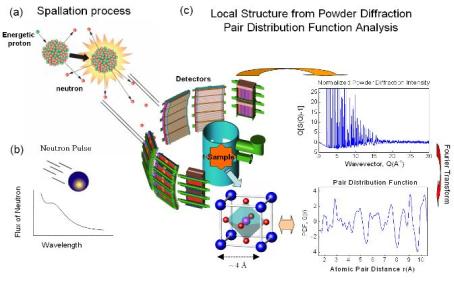
펄스 중성자 분말 회절실험은 현재 영국, 미국, 그리고 일본 등의 여러 나라에서 수행되고 있다. 먼저 펄스 중성자를 만들기 위해서 양성자 펄스를 고에너지 (수백 MeV)로 가속시킨 후 액체 수은함에 입사시킨다. 이 때 수은의 원자가 깨어지면서 다량의 중성자 펄스가 발생한다. 이런 원자핵의 파쇄 과정 (spallation process)을 그림 3(a)에 개략적으로 표현하였다 [9]. 이렇게 발생한 중성자 펄스를 감속제를 써서 실험에 사용하기에 적당한 에너지를 가지도록 에너지를 감소시켜 준다. 그림 3(b)는 중성자 펄스의 개략적인 파장과 중성자 다발 (flux) 그래프이다. 여기서 알 수 있는 사실은 상대적으로 에너지가 큰 중성자의 다발이 훨씬 많다는 것이다. 파동벡터 Q는 파장에 반비례하기 때문에 파장이 짧을수록, 즉 에너지가 클수록 큰 파동벡터를 얻을 수 있어 퍼짐산란을 이용한 원자 배열의 단거리 질서 연구에 용이하다. 그림 3(c)는 펄스 중성자를 이용한 분말 회절실험 장치 개략도이다. 입사하는 중성자 펄스가 넓은 에너지 대역을 가지고 있기 때문에 특정 위치에 고정되어 있는 검출기에서 넓은 영역의 분말회절 패턴이 측정된다. 측정된 분말회절 패턴은 흡수 및 이중 산란 등에 대한 보정과 규격화를 거친 다음 실공간으로 퓨리에 변환하여 atomic pair distribution function (PDF) 스펙트럼을 얻게 된다 [5]. PDF 스펙트럼에서 픽의 위치는 원자간 거리에 해당되기 때문에 실공간에서 원자 배열을 이해하는데 아주 유용하며 브래그픽과 퍼짐산란 모두를 실공간으로 퓨리에 변환하였기 때문에 원자배열의 장거리 질서뿐만 아니라 단거리 질서에 대한 정보를 포함하고 있다.

그림 3. 원자핵 파쇄과정 (Spallation process)을 이용한 펄스 중성자 발생과 [9] 이를 이용한 분말 회절실험 장치. 분말 회절 패턴을 실공간으로 퓨리에 변환하여 PDF 스펙트럼을 구할 수 있다. PDF 스펙트럼을 이용하여 실공간에서 원자배열의 단거리 및 장거리 질서를 연구할 수 있다 [5].

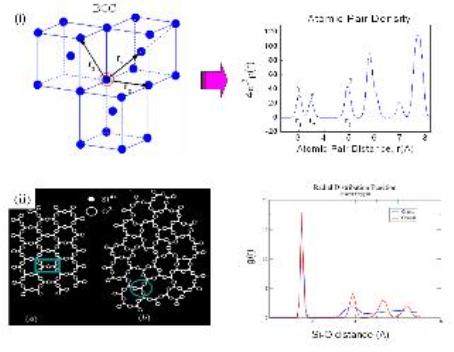
여기서 PDF 스펙트럼에 대해 좀 더 알아보자 [5, 10]. PDF 스펙트럼은 말뜻이 의미하는 바와 같이 원자들의 밀도 분포를 나타낸다. 즉, 어떤 기준 원자로부터 또 다른 원자를 발견할 확률을 나타낸다. 그림 4(i)의 BCC (body-centerd cubic) 결정의 예를 들어 보자. 먼저 BCC 결정의 한 원자를 기준 원자로 잡아준다. 그 다음 기준 원자로부터 반경 r인 구면위에 또 다른 원자가 발견될 확률을 계산한다. 가령, 반경 r 값이 최인접 원자간 거리보다 작으면 PDF값은 0이 된다. 반경 r 값이 점점 커져 최인접 원자간의 거리에 근접하게 되면 그림 4(i)에서와 같이 픽이 나타난다. 그 다음 두 번째 인접 원자간 거리, 세 번째 인접 원자간 거리에서 픽이 나타나게 된다. PDF 픽의 반치폭 (peak width)은 원자들의 열적운동이나 정적 무질서에 의해 결정 된다. 그리고 각각의 PDF 픽 아래의 면적을 계산하면 배위수 (coordination number)를 구할 수 있다. 하지만 기준 원자로부터 반경이 점차 커지면서 원자간 거리가 비슷한 원자쌍들이 존재하게 되어 PDF 픽은 여러 원자간 거리의 중첩으로 나타난다. 또 한 가지 주의해야 할 사항은 분말 회절 패턴의 퓨리에 변환에 의해 구해지는 PDF 스펙트럼은 분말 평균으로 인해 원자간 거리에 대한 정보만 제공하고 방향에 대한 정보는 제공하지 않는다. 하지만 PDF 픽의 모양과 상대적인 세기의 차이, 두 번째 인접원자간 거리등을 이용하여 3차원적인 원자 배열에 대한 정보를 재구성할 수 있다.

원자 배열의 장거리 질서가 있는 경우와 단거리 질서만 있는 경우 PDF 스펙트럼은 어떻게 나타날까? 그림 4(ii) 는 SiO2 결정과 SiO2 유리의 원자 배열을 평면에 나타낸 것이다. 먼저 결정의 경우 Si 원자 주위의 O 사면체가 규칙적으로 반복됨을 알 수 있다. 하지만 유리의 경우는 Si 원자 주위의 O 사면체가 존재하기는 하지만 이들 상호간의 규칙성은 존재하지 않는다. 따라서 이 두 경우의 원자 배열을 실공간에서 PDF 스펙트럼을 이용하여 비교하면 최인접 Si-O 원자간 거리에 해당하는 PDF 픽은 아주 잘 일치한다. 하지만 유리의 경우는 두 번째 인접한 Si-O 원자간 거리부터는 PDF 픽의 반치폭이 매우 커지며 PDF 픽들간의 경계가 불분명해 진다. 만약에 SiO2 결정과 유리의 원자배열을 모르고 있었다면 PDF 스펙트럼으로부터 두 물질 모두 잘 정의된 SiO4 사면체로 구성되어 있으며 결정의 경우는 SiO4 간의 규칙성이 있으나 유리의 경우는 규칙성이 없음을 알 수 있었을 것이다.

그림 4. 실공간에서 PDF 스펙트럼에 대한 개념도. (i) BCC 결정의 결정구조 모델. 먼저 원자 하나를 기준 원자로 정한 후 기준 원자로부터 반경이 r인 구면에 또 다른 원자들이 존재하는지를 확인한다.

다음은 원자 배열의 장거리 질서와 단거리 질서가 서로 다른 경우를 살펴보자. 전형적인 강유전체인 BaTiO3는 산소 팔면체의 중심에 놓여 있는 Ti 이온의 변위와 이에 따른 단위낱칸의 변형에 의해 원자 배열의 장거리 질서가 바뀌게 된다. 즉 온도가 낮아짐에 따라 cubic 결정구조의 Ti 이온이 [001] (z 방향), [110] (x-y 방향), 그리고 [111] (x-y-z 방향) 으로 이동하면서 각각 tetragonal (T )구조, orthorhombic (O) 구조, 그리고 rhombohedral (R) 구조로의 상전이가 생기는 것으로 알려져 왔다 [12]. 이 경우 Ti 이온의 단거리 질서와 장거리 질서가 일치하게 된다. 하지만 최근의 연구결과에 따르면 Ti 이온은 항상 <111> 방향으로 이동하며 8개의 서로 동등한 <111> 변위들이 서로 그룹을 지어 평균적으로 온도에 따라 T-O-R 구조로 상전이가 일어난다는 것이 실험과 이론적 계산을 통해 제안되었다 [13, 14]. 이와 같이 장거리 질서와 단거리 질서가 서로 다른 때는 원자 배열의 장?단거리 질서를 동시에 분석하여야만 물성을 보다 잘 이해할 수 있다.

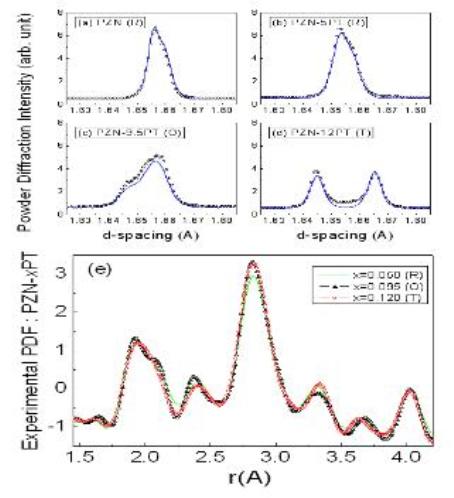
그림 5은 원자 배열의 장거리 질서와 단거리 질서를 종합적으로 연구한 사례를 보여준다. 먼저 (a-d)는 릴랙서 강유전체인 (1-x)Pb(Zn1/3Nb2/3)O3-xPbTiO3 (PZN-xPT)의 조성에 따른 회절 패턴이다. PbTiO3의 양 x가 증가함에 따라 브래그픽의 모양이 달라짐을 알 수 있다. 브래그픽의 위치와 세기를 분석하는 Rietveld 분석 결과 [15] PZN-xPT의 장거리 질서는 x 값에 따라 rhombohedral (R), orthorhombic (O) 그리고 tetragonal (T)로 결정구조 상전이를 한다는 사실이 밝혀졌다. 이러한 실험적인 결과와 제1원리 계산을 바탕으로 전기분극의 회전이 스트레인 발생의 주된 메카니즘으로 제시 되었다 [16]. 하지만 그림 5(e)의 PDF 분석 결과는 PZN-xPT내의 단거리 원자배열이 PbTiO3의 양에 거의 의존하지 않음을 보여준다. 따라서, PZN-xPT의 장거리 질서가 PbTiO3의 양에 따라 R-O-T로 상전이 할 때 국소 전기 분극을 나타내는 단거리 질서는 변하지 않음을 의미한다. 이러한 결과는 앞에서 서술한 BaTiO3 의 경우와 매우 유사하다. 따라서 전기분극의 회전에 의한 결정구조 상전이 보다는 항상 존재하는 국소 전기분극이 서로간의 질서 또는 무질서 배열을 이룸에 따라 결정구조 상전이가 일어난다고 보는 것이 합당할 것이다 [11].

그림 5. (a-d) (1-x)Pb(Zn1/3Nb2/3)O3-xPbTiO3 (PZN-xPT) 의 조성에 따른 중성자 분말 회절 패턴. (e) PZN-x PT의 조성에 따른 PDF 스펙트럼 [11].

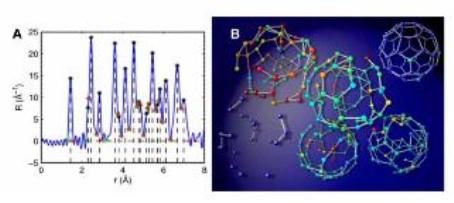
마지막으로, 최근에 PDF 스펙트럼으로부터 고체 상태의 나노구조를 ab initio 방법으로 재구성하는 알고리듬이 개발 되었다. 그 예로 그림 6은 PDF 픽의 위치와 세기로부터 C60의 3차원 모델을 만들어 가는 과정을 보여준다. 그림 6(B)의 왼쪽 아래에서 오른쪽 위쪽으로 점차적으로 C60의 원자모형이 완성되어 가는것을 보여준다. 이 결과는 PDF 스펙트럼과 컴퓨터 알고리듬만을 이용하여 나노물질의 구조를 Å이하의 정확도로 결정할 수 있음을 보여주어 나노물질의 구조 연구에 신기원을 열었다고 할 수 있다 [17].

그림 6. A) 원자간 거리와 다중도 정보를 얻기 위해 사용된 PDF 스펙트럼. (B) PDF 스펙트럼을 이용하여 만들어진 C60 모델. 왼쪽 아래에서 오른쪽 위쪽으로 점차적으로 모델이 완성되어가는 중간 과정을 보여준다. (출처: P. Juhas et al., Nature 440 655 (2006)).

[5] T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks Structural Analysis of Complex Materials (Pergamon, 2003).
[9] https://str.llnl.gov/index.html
[10] http://www.totalscattering.org
[11] I.-K. Jeong et al., Appl. Phys. Lett. 92, 172911 (2008).
[12] F. Jona and G. Shirane, Ferroelectric Crystals (Pergamon Press, 1962), Chap. IV.
[15] R. A. Young ed., The Rietveld Method (Oxford Univ. Press, 1993).
[16] H. Xu and R. E. Cohen, Nature 403, 281 (2000).
[17] P. Juhas et al., Nature 440 655 (2006).